Acoustics and Psychoacoustics
Music is probably the most intangible of all the art forms, and yet it is probably the most powerful. Defining its boundaries has for centuries proved contentious, for music is a cultural form and is not drawn from nature. As Lévi-Strauss remarks:
Whereas colours are present 'naturally' in nature, there are no musical sounds in nature, except in a purely accidental and unstable way; there are only noises.
This statement implies a distinction between 'music' and 'noise', the one ordered, the other chaotic. As we shall see, such distinctions are harder to justify when we look in microscopical detail at the sounds which are described as musical, for orderly and disorderly elements are to be found at every level of musics of every culture.
Although music primarily reaches the brain from the ears, this is by no means the only route. Most people will have experienced the visceral sensations produced by an orchestra playing fortissimo, or a loud disco: there can be a stage when our ears become fully saturated and music is no longer heard, but felt. Some deaf people exhibit profound musical skills and extraordinary sensitivity - several years ago I met a recently-graduated musician who, although deaf, was an organist and choirmaster. He had an exquisite sense of pitch which I tested by playing musical intervals and chords to him in a number of tuning systems. Even at low dynamic levels he was able to discriminate between very small discrepancies in intonation very accurately. He indicated to me that his 'hearing' seemed more acute when he removed his glasses, suggesting that the body attempts to find other routes to the brain when the main route is broken.
For most of us, however, the ear will form the primary means by which sound is received and transformed to the electro-chemical signals which the brain uses. Before we can discuss this transformation, however, we must consider what sound is on the most primitive level: what actually passes from musical instrument, voice or loudspeaker to the ear of the listener. Sound is transferred from the musical source to the ear by the motion of the molecules which form the air. It should be noted that the individual molecules themselves travel very small amounts, although sound can travel over very great distances. A useful analogy to the motion of the air molecules can be found in the 'slinky spring', the children's toy made from coils of plastic or metal which can 'walk' down stairs. If the two ends of the spring are pulled some distance apart and held horizontally, and one end is given a slight push, a pulse will be seen travelling up and down the coils as one-by-one the individual sections move forwards then back.
Sound energy and waves
What is transmitted by the motion of the air molecules is energy, in a form described as sound energy. The transmission of sound takes the form of a wave which spreads out from the sound source rather in the way that ripples in water do when we drop a pebble in it. Air molecules close to the sound source are initially compressed (pushed together) and rarefied (pulled apart), and the wave travels out from the source gradually losing energy.
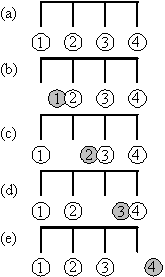
Figure 1. An idealized picture of the displacement of four air molecules at five successive instants of time.
The process is illustrated in a highly idealized way which should not be taken too literally in Figure 1. At first (a) all four molecules are stationary, then (b), the first molecule is pushed forward and interacts with the second molecule. As the second molecule pushes forward (c), the first moves back to its first position. The second molecule then moves back (d) while the third is pushed forward. Finally the position of the third molecule is restored (e) as the fourth is pushed forward. This process of radiation of the sound wave takes place three dimensionally - the pressure wave moves outwards spherically from a point source like a musical instrument.
If we had some sort of meter which could register the change of pressure at a distance from the sound source, we would notice that it was constantly changing, up and down around a fixed point. As the air was compressed, the pressure would rise, and as it was rarefied, it would fall. If these pressure changes were to be drawn out on a piece of paper, we would tend to find patterns emerging, especially if the changes of pressure were in response to sustained pitched notes from a musical instrument such as a recorder (Figure 2).
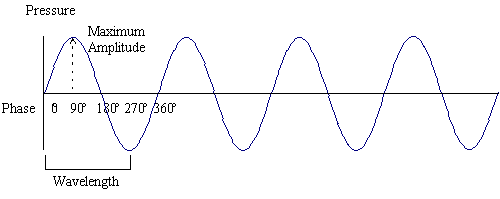
Figure 2. Pressure changes over time of a simple tone.
The shape which emerges in Figure 2 has something of the appearance of the ripples found on water, with a repeating pattern of successive crests and troughs. This kind of diagram should not be misunderstood as a depiction of the motion of the air molecules, however, but as a way of imagining the train of pressure changes which travel from the source to the listener. If we connect a microphone through an amplifier to an oscilloscope, we will actually see a display of how the voltage produced by the microphone changes over time, and as we shall see in chapter two, this change is analogous to the change of air pressure. The waveform shown in Figure 2 is described as a sine wave, and is the simplest waveshape found in music, having a rather bland sound; most synthesizers can produce sine waves, but use them as building blocks for more complex sounds.
Frequency, wavelength and period
The waveshape will repeat many times, the number of repetitions per second being described as its frequency. The note A above middle C that orchestral musicians tune to has, for example, a frequency measured in hertz of 440 Hz (Hz is the abbreviation for hertz), in other words the complete waveshape recurs 440 times each second. Lower frequencies result in lower pitches, and higher frequencies in higher pitches. The other two basic characteristics of a waveform are its wavelength and its amplitude, both of which are illustrated in Figure 2. The wavelength of a wave is a measure of the length of a single waveshape in metres, and the period is the length of time taken by one complete wave. Sound travels at roughly 343 metres each second, thus, for a sound whose frequency is 440 Hz, its wavelength is 343/440 metres (0.78 m), and its period is 1/440 seconds (0.0023 seconds). Phase is measured in degrees from 0º - 360º (see Figure 2) and represents the position in the wave. If the sine wave in the Figure was to be moved forward 180º, it would be turned upside down (the peak would be come the trough and vice versa).
The maximum amplitude (or 'height' of the wave) is a measure of how much the air is compressed, and thus how loud it will sound. As can be seen from the figure, the amplitude is constantly varying above and below a threshold point which represents normal air pressure: the greater the maximum amplitude, the louder will be the sound, though as we shall discover, the relationship between amplitude and loudness is not clear cut. As a rule of thumb, the tripling of a sound's amplitude may often have the effect of making it sound roughly twice as loud.
If we think about a stringed instrument like a guitar, it is quite easy to see how the vibrations transmitted through the air are established, for if we pluck the lowest string on a guitar (E2) we can actually observe the backward and forward motion of the string which alternately compresses and rarefies the air around it. The motion of the is the result of an impulse repeatedly running up and down the string forming a standing wave. The frequency of vibration of the string, and thus its musical pitch, is dependent on several factors: its length - the shorter the string, the higher the pitch; its thickness and mass - the thicker and more massive the string, the lower the pitch; and its tension - the tighter the string, the higher the pitch. In the case of the guitar, all the strings are the same length between the nut and the bridge, though the top and bottom strings are tuned two octaves apart. This is accomplished by making the strings gradually thinner and at higher tension from the lowest strings to the highest.
If the string, once plucked, is allowed to vibrate freely, its oscillations will gradually diminish and the resultant sound will decay because of friction. If we want a string instrument such as a violin or cello to sustain longer than its natural vibrations permit, we must somehow continue to supply it with energy; this is normally accomplished by using a bow, which successively drags and releases the string it as it is drawn across it.
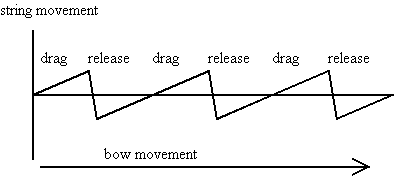
Figure 3. The cycle of drag and release of the string of a violin under the influence of a resined bow.
Complex sounds
The sound produced by a string instrument is usually considerably more complex than the simple sine wave described above. This is because of the presence of frequencies other than the fundamental frequency (the one that causes us describe the note as middle C or whatever) which are variously called harmonics, partials or overtones. The timbre or tone colour of a sound is dependent upon the relative loudness at any point in time of a series of harmonics, all of which can be thought of as sine waves. A string not only vibrates as a whole as in Figure 4 (top illustration), but in halves, thirds, quarters and so on (Figure 4, lower three illustrations). If a finger is very lightly placed at various points on a guitar string on one of the so-called nodes marked N in the figure, the string can be forced to vibrate in one of the ways illustrated. By gently placing a finger so that the pad is just touching the string half way down its length, near the twelfth fret (the lowest E string is usually the most successful for the novice guitarist), and plucking as normal with the other hand, a note one octave higher than the open string, but with a much thinner tone colour, will sound. If a finger is placed near the seventh fret, where it would normally sound a perfect fifth higher, the string is forced to vibrate in three sections like the third illustration of Figure 4, and a note one octave and a fifth higher than E2 will sound. The string can be divided into four by placing a finger near the fifth fret and playing, resulting in a note two octaves higher than the open string.
The four illustrations in Figure 4(a) represent the first four elements in a sequence of whole numbers called the harmonic series, which is, at least theoretically, infinite. It will be seen from Figure 4, and the discussion above, that there is a mathematical relationship between the harmonic number and its frequency relative to the fundamental (E2 in Figure 4(b)). In fact, the frequency of the harmonic equals its number in the harmonic series multiplied by the frequency of the fundamental.
Thus, using Figure 4(b) as an example, given that the frequency of E2 is 82.4 Hz, the frequencies of the next three harmonics are:
82.4 2 = 164.8 Hz (second harmonic)
82.4 3 = 247.2 Hz (third harmonic)
82.4 4 = 329.6 Hz (fourth harmonic)
The series continues on after the eighth harmonic with gradually smaller intervals, through roughly major and minor seconds to microtones. It is important to note that for each musical octave there is a doubling of frequency, thus for a tone of 220 Hz (A3), the next three octaves will be 440 (A4), 880 (A5) and 1760 Hz (A6). The difference in frequency between each note will therefore increase the further up musical space we move.
Modes of vibration and resonance in string instruments
The vibration of a real string is the result of the addition of the different modes of vibration illustrated (and many more) at different amplitudes, and thus any single sound is a essentially a kind of chord formed from harmonics. We shall consider later in this chapter how the ear integrates the information as a single 'note'. It is important to realise that a string suspended in the air between two posts which is plucked or played will produce next to no sound. Some form of resonator is required to amplify the sound generated by the string, and this is usually an elaborately curved box with air holes in it. The front and back plates of the violin and the air cavity between them all have their own characteristic resonances (modes of vibration), which the motion of the strings excite, and in a sense the string instrument can be regarded as a kind of wind instrument. The actual tone colour that a string instrument produces is largely dependent upon the method of its construction, and the quality of its components - the choice of woods, glues and so on.
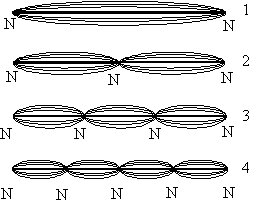
Figure 4 (a). The first four modes of a vibrating string.
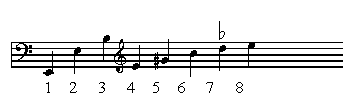
Figure 4 (b). The first eight harmonics of the harmonic series on E2. Note that the seventh harmonic is slightly flatter than D.
The time domain and frequency domain
Acousticians and engineers employ two different methods of describing sound: as time-domain information and as frequency-domain information. Time-domain methods involve the plotting of pressure or amplitude variations against time as waveforms, and make use of graphic representations such as Figure 2. Frequency-domain methods are concerned with the relative amplitudes of the harmonics which make up a sound, and are usually displayed in graphs like that of Figure 5. Such graphs, called harmonic spectra (singular spectrum), depend upon a special mathematical procedure called Fourier Analysis to generate their data, whose methodology is beyond the scope of this book. They represent short snapshots of the sound, and a number must be taken to give an idea of how the sound evolves and changes over time.
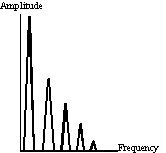
Figure 5. A frequency-domain analysis of a sound.
Sound production in wind instruments - the open pipe
The mechanism for sound production in wind instruments is somewhat harder to picture than that of string instruments, though a column of air vibrates in an analogous way to the string described above. If we first consider a cylindrical pipe which is open at both its ends (a simple flute-like instrument), and refer back to Figure 1, we will note that an increase in air pressure at one end of the pipe (caused by blowing a puff of air) will pass down the pipe as a longitudinal wave. When the wave reaches the other end of the pipe, a little of its energy will be released, but most of it will be reflected back up the pipe as a negative pulse, rather like a ball rebounding from a wall it has been hit or thrown at (Figure 6).

Figure 6. An impulse and its reflection in an open tube.
When the impulse is half way down the length of the tube, the air pressure in the tube will be at its maximum positive value (being farthest from the open ends), and when the reflected pulse is at the centre, pressure will be at its maximum negative value; at the ends of the tube, the air pressure will be the same as that outside the tube. Considering the slinky-spring model again, the high-pressure condition is analogous to the position where the coils of the spring are pressed close together, and the low-pressure condition is equivalent to the ends of the spring being stretched apart. If we were to draw a picture of these changes we would see, in the simplest of cases, a graph like Figure 2.
Another useful model is provided by the executive toy called a Newton's cradle, which consists of a series of (usually five) closely-spaced steel ball bearings suspended in a line at the same height from a frame. If a ball bearing from one end is pulled back slightly and released, it will move forward and strike the ball in front transmitting its energy to it. The energy will be passed down the line with the middle three balls scarcely moving. The final ball will be pushed forward almost to the extent to which the first ball was pulled back, and then fall back repeating the chain of events in reverse. The outer balls will continue 'clicking' to and fro for some time, before friction slows the simple machine to a halt. If the inner balls are investigated carefully, they will be seen to oscillate very gently, while outer balls swing much more widely. This is analogous to the condition in Figure 4(a), top diagram, where the pressure is least at the extremes (the balls are displaced most), and most in the centre (the balls are displaced least).
To return to the open pipe, a complete trip down and up its length is required for the impulse to complete one cycle of the waveform, and thus the fundamental wavelength will be twice the length of the tube. A flute is around 62 cm in length, which would imply that the wavelength of its lowest note (C4) is 62 * 2 = 124 cm. In actual fact, for various reasons, including so-called end-correction (a kind of overshoot which is not dissimilar to the behaviour of the outer balls in the Newton's cradle model), the actual wavelength is 132cm. Like string instruments, open pipes (flutes, recorders, penny whistles and so on) support not just a single harmonic, but a series of them. Thus the vibration pattern within the tube and the waveform will be a complex mixture of the vibration patterns of the individual ingredients.
As with string instruments, a means is required to continue giving energy to the column of air in the tube to maintain its vibrations. Although a continuous stream of air is blown over the embouchure (the French word for mouthpiece) of a flute, the air flows in as if controlled by a valve. Comparing the air flow to the four stages of a sine wave as depicted in Figure 2, it will be noticed that at the first stage little air flow in. As maximum pressure is approached , air flows in at much higher pressure, which reduces as the midline is approached. At the pressure minimum, the valve effectively closes, preventing air intake, and moving back to the midline, air is admitted again. This is, of course, a crude description of what is actually a much more complicated pattern of air flow. With increasing air pressure caused by blowing harder on any note on an open pipe (for instance, the lowest note on a recorder) it is possible produce notes from the harmonic series. A descant recorder whose lowest note is C5 will sequentially produce C6, G6, C7, E7, and G7 when overblown. Blowing beyond the first six or so harmonic is usually both difficult, and ear-piercing if successful!
Sound production in wind instruments - the closed pipe
A cylindrical tube which is stopped at one end functions in a rather different way to the open pipe. As can be seen in Figure 7 (a), there are four stages in a complete cycle of an impulse. The upper two dashed lines represent conditions that are analogous to those found in the open pipe, the positive pulse being reflected back as a negative one from the open end. When the reflected wave meets the closed end of the pipe, it is now reflected as a negative pulse, and when the reflected negative pulse reaches the open end it reflects as a positive pulse. As the pulse has travelled the length of the pipe four times, its wavelength will be approximately four times the length of the pipe, in other words a 30 centimetre pipe will have a wavelength of around 120 cm, twice that of the flute, and sounding one octave lower.
Pressure patterns for the first and second mode are illustrated in Figure 7 (b). In the upper diagram it will be seen that only half a full wave is present, and in the second one and a half waves. Given that two complete passages up and down the pipe are required to complete one cycle, the illustrations suggests why the fundamental frequency of the pipe is the same as an open pipe of twice the length. Interestingly, the second mode will have a frequency three times that of the fundamental, and the third mode five times. Thus a stopped pipe misses out even numbered notes of the harmonic series, and overblowing initially produces a note which is one octave and a fifth higher.
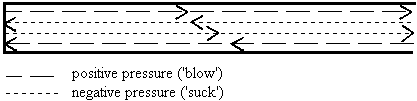
Figure 7(a). An impulse and its reflections in a closed pipe.
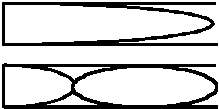
Figure 7(b). First and second pressure modes for a pipe closed at one end.
The clarinet, a cylindrical tube with a rather narrow bore, has one end effectively closed by a mouthpiece with a single reed. The reed acts like a valve which opens or shuts depending upon the pressure inside the pipe, in a somewhat similar way to the 'air-valve' of the flute. The frequency of its vibrations is largely dependent upon the resonant frequency of the air column in the instrument, a feature which physicists describe as coupling. The sympathetic vibration of strings in a piano when the pedal is lifted is another common example of coupling. The lowest written pitch for the clarinet is E3, which means that overblowing will produce B4, a twelfth rather than an octave higher; the gap between Bb4 and B4 is known as the break, the point which separates the lower two registers. Because the clarinet supports only odd-numbered members of the harmonic series, it produces a characteristically 'hollow' timbre.
Wind instruments with a conical bore
So far we have considered pipes with a cylindrical bore. Other woodwind instruments, for example oboes and bassoons, employ pipes with a conical bore. Although these are closed at one end by a double-reed valve mechanism, they behave in many ways like open pipes of the same length, and support both odd and even members of the harmonic series. The double reed functions like the single reed of the clarinet, its frequency similarly being dependent upon the resonances of the air column, but it takes considerably more stamina and expertise to control.
If a brass instrument were a simple cylinder, it would behave like the stopped pipe of a clarinet, producing only odd-numbered harmonics. The trumpet, horn and trombone all have conical sections: in the case of the trumpet this is a little less than two thirds of the tube length, for the French horn it is slightly less than one half, and for the trombone it is somewhat more than one third. The effect of this, the flared bell and the mouthpiece is to cause the instrument to have the characteristics of an open pipe producing all the harmonics of the harmonic series. The valve mechanism controlling air intake is formed by the player's lips, and is similar in function to that described above for woodwind instruments.
Formant regions
A feature of the tone colour of most musical instruments is the presence of formant regions. These are frequency areas which are particularly prominent components of the overall sound, and are common to many or all notes played: they can be regarded as 'fingerprints' of an instrument giving it its own idiosyncratic character. Essentially they are a kind of filter (a concept to be discussed in fuller detail later in this volume) which selectively amplifies or attenuates some parts of the sound, and can be compared to a sieve which allows particles smaller than the diameter of the mesh to pass through. In speech, the shape of our vocal tract (the pharynx, the mouth, the nose and the sinuses) is altered in order to produce different vowel sounds, and associated with each vowel is a set of formant frequencies. Acousticians tend to categorize vowel sounds by the formant frequencies, which are different in pitch for men, women and children (because of the difference in size of the tract). Thus, for instance, the first three formants for a man saying the vowel sound 'ah' are (on average) around 730 Hz, 1090 Hz and 2440 Hz respectively, the first formant intensity being roughly two and a half times that of the second and five hundred times that of the third.
In effect the vocal tract is a wind instrument of the stopped-pipe variety, with the vocal chords acting like the double reed of the oboe, and the vocal organs being the resonator for the air column. The formant frequencies 'shape' the sound output so that it is louder around the formants and quieter elsewhere, acting as kinds of focuses. When vowels are sung, the formant frequencies may be considerably altered, and a further 'singer's formant' between 2500 and 3000 Hz introduced. As we shall discover when we consider hearing in more detail, this is a frequency region to which the ear is particularly sensitive.
Percussion instruments and non-harmonic partials
The instruments discussed so far produces sounds with harmonically-related content, in other words the overtones are from the harmonic series. Percussion instruments can produce sounds with much more complex structures than string, brass or woodwinds, often involving substantial noise elements, and non-harmonic (inharmonic) partials (ones which are not whole-number multiples of the fundamental frequency). As an example of this, the marimba has a second partial frequency which is 3.9 times its fundamental, and a third partial which is 9.2 times its fundamental. The membranes found in drum heads produce complex modes of vibration (called Chaldni patterns) which, ideally, have the following ratios for the first twelve partials:
Ratio 1 1.59 2.14 2.30 2.65 2.92 3.16 3.50 3.60 3.65 4.06 4.15.
Real drums have slightly different ratios from the ones above, because of the effect of the air enclosed within the body of the instrument.
The ear and the reception of sound
If sound is energy created by a vibrating body and amplified by a resonator which is transmitted through the air as a changing patterns of pressure, how is it then received and processed? There are three functional sections of the ear, described as outer, middle and inner respectively, and each plays a different role in the reception of sound and its conversion into electrical impulses for processing by the brain (Figure 8).
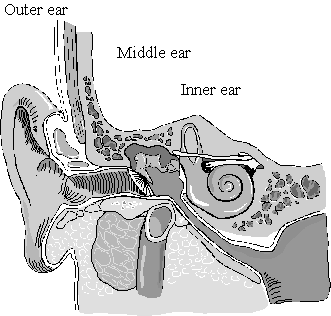
Figure 8. The ear.
The outer ear consists of the visible pinna and a canal called the auditory meatus leading to the eardrum. The main role of the pinna, with its strange furrows and convolutions, is to help localize high frequency components of sounds. It appears that, the pinnae act as filters, changing the high-frequency harmonic content of the sound above 6000 Hz, depending upon the angle at which it strikes the ears. The meatus (Latin for way or path), or ear canal, is the short tube of around 2.5 - 4 cm in length in an adult, which lies immediately inside the pinna, and which is closed at one end by the eardrum. It is thus effectively a stopped pipe which has a resonant frequency of around 3400 Hz.
The sound waves reach the eardrum, a thin membrane at the end of the meatus, setting it into motion like the skin of the drum. Thus the pressure changes in the air are turned back into kinetic (movement) energy, an example of a kind of transduction which will be the focus of chapter two. The middle ear is an air-filled cavity with three of the smallest bones in the body, the hammer, anvil and stirrups, and a passage called the Eustachian tube which allows air to enter and exit. If the Eustachian tube becomes blocked, either by catarrh or a sudden change of pressure such as happens when an airplane takes off or lands, strange feelings of fullness or odd clicks and buzzes can be felt in the ear. The tiny bones within the cavity are connected on one side to the eardrum, and on the other to a similar but smaller membrane on an opening on the inner ear called the oval window. The function of the bones is to amplify the tiny movements of the eardrum to much larger ones on the oval window.
The inner ear, or cochlea, is a coiled up shell-like fluid-filled organ. Liquid is much harder to compress than air, and in technical terms has a greater impedance or resistance to compression, thus the hammer, anvil and stirrups also match the impedances of air and liquid. Example 9 schematically illustrates the main components of the uncoiled cochlea: the round and oval windows, the tectorial membrane and the hair cells. The organ has a kind of 'sandwich' organisation with upper and lower fluid-filled sections connected by a small gap called the helicotrema surrounding a central 'filling' containing a membrane (the tectorial membrane) in contact with, or at close proximity to hair cells which convert the movement of the tectorial membrane into electrical impulses. In essence, the vibrations passed from the oval window cause the tectorial membrane to move in rather the way a stretched rope does when a sharp flick is given at one end. A travelling wave passes down the membrane reaching a maximum at a certain point along its length, causing the hairs embedded in the hair cells at that part of the membrane to be displaced, and in simple terms, this displacement causes the firing of nerve impulses. The membrane can be imagined as being like a piano keyboard in the sense that each section of it is responsible for a specific frequency, with high-frequency response being associated with the hair cells nearest the windows, and low-frequency response with those nearest the helicotrema.
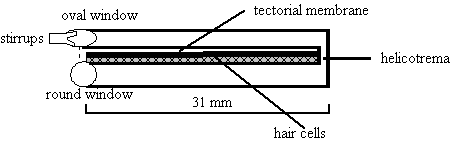
Example 9. The inner ear - schematic diagram (not to scale).
The explanation of frequency perception described above, in which each part of the tectorial membrane responds to a different range of frequencies, is known as a place theory. Another explanation which relies on how fast the nerve cells fire is called temporal coding, or phase locking. It has been discovered that for many frequencies, nerve cells respond by firing at the period of, or a multiple of the period of the sound being heard. Thus for a 100 Hz tone, whose period is one hundredth of a second, nerves may fire at intervals of 1/100 second, 2/100 second, 3/100 second and so on.
If a musical tone in most cases actually consists of a series of harmonics, how do we manage to hear it as a single sound rather than as a set of separate pure tones? It has been discovered that even when the fundamental frequency of a sound is missing, but other components of its harmonic series are present, the ear (or brain) can detect the fundamental frequency (called its 'virtual pitch'). It can be deduced that, at some or all levels of the reception and processing of sound, there is an inherent 'expectation' of sounds to conform to the pattern of the harmonic series. Thus, when we hear a triad of C major played by three instruments, each note will contain both its own harmonic series which is distinct from the other two, and its own characteristic formant, which enables its separation as a discrete sound.
The limits of hearing
It is not possible to give hard and fast frequency limits for human hearing. Most Hi-fi companies stress that their equipment will reproduce frequencies between 20 and 20000 Hz (roughly 10 octaves), implying that we are able to hear within this range. In most cases adults will have rather more restricted hearing, which will tend to reduce with age, and an upper limit of 15000 Hz is possibly more reasonable.
Loudness detection is largely associated with the rate at which the nerve cells fire. Generally speaking, the louder the sound, the greater the frequency of nerve cell impulses, up to a point when the sound is so loud, the response saturates and louder events cannot be detected as such. There is some controversy about nerve and hair-cell damage due to contact with loud sounds over prolonged periods. Most people will be familiar with the temporary hearing loss following exposure to very loud music in discos or rock concerts. This brief loss can perhaps be equated with the muscle fatigue produced by strenuous exercise, and can involve auditory fatigue a change in the threshold of hearing (the quietest sound we can hear), and temporary auditory adaptation (sounds do not seem as loud). It should be noted that the threshold of hearing which has been discovered experimentally may not conform to that we experience in everyday life, because quiet sounds are often masked by environmental noise.
Extended periods of contact with loud noises can produce a much more serious condition in which the threshold of hearing rises and the adaptation is permanent. Equally disturbing, and perhaps even more debilitating, is the condition called tinnitus, in which the sufferer periodically or continuously hears a particular, often high pitched, musical sound. There have been reports of sufferers whose condition began or deteriorated after contact with heavily amplified music, though some professional musicians claim that, while prolonged contact with noise may be dangerous, music is less hazardous.
Loudness, amplitude and decibels
The term loudness describes a subjective sensation; we will now consider its objective 'scientific' equivalents, namely amplitude and intensity. It was noted earlier that the amplitude was a measure of the pressure of a wave, and it is a remarkable fact that the sound with the highest pressure that a normal person can hear (the threshold of pain) is some million times greater than that of the threshold of hearing. The enormous range of numbers associated with these pressure changes proved difficult to deal with, and a logarithmic scale called the decibel (dB) was introduced. The term decibel was named after Alexander Graham Bell, the inventor of the telephone, and literally means one tenth of a bel. It is a widely used term in audio engineering and compares a measured value to a known reference value (for example the threshold of hearing).
To find the decibel value of a sound pressure level the following method is used:
1. The measured value is divided by the known value;
2. The logarithm is taken of the result of stage one using a calculator;
3. The result of stage two is multiplied by 20.
In mathematical terms this is expressed as
![]() .
.
It should be remembered that logarithms deal with mathematical powers, in this case powers of ten. If we take as an example the number 100, this can be expressed as 102, and its log as 2 - the same value as the power (exponent). The log of 1000 is 3 (103), and of 1/10 is -1 (10-1). Intermediate values between powers of ten will include a decimal part, thus the log of 256, which is between 100 (102) and 1000 (103) is 2.408. Although the maths may seem perplexing or confusing, it is important to remember that adding 6 dB to a sound pressure value is the equivalent of doubling it, and subtracting 6 dB is the equivalent of halving it. Thus if a sound has a pressure level which is 24 dB higher than another, it is actually sixteen times greater (24/6 = 4, 2*2*2*2 = 16). Adding 10 dB to the sound pressure is equivalent to multiplying the pressure by about three. The range of audio sound pressure levels varies from 0 dB SPL (Sound Pressure Level), the threshold of hearing, to around 120 dB SPL.
When two sounds with equal sound pressure level (for instance two violins playing the same part) are sounded together, the resulting increase in SPL is 3 dB, and each time the number of instruments doubles, 3 dB is added to the overall sound pressure level, thus if two violins each playing at 60 dB produce a total of 63 dB SPL, four violins would produce 66 dB SPL, and 8 violins would produce 69 dB. In reality, there are sufficient differences between instruments in terms of vibrato amount, phase position and noise to make such simple calculations rather unreliable.
Intensity and power
Although sound pressure level is a useful measurement in that it indicates the level of the sound striking the eardrum, measures of the sound's intensity or its power are often used. Sound power, as shall be discussed in chapter two, is commonly used in association with the output from loudspeakers, and indicates how much energy flows over a period of time (we noted earlier in this chapter that energy was transmitted by the movement of air molecules caused by the sound wave). Sound power changes in the same way that sound pressure does, and is also measured in decibels, so that a 6 dB increase in pressure will in general produce a 6 dB rise in power. Rather confusingly however, for power and intensity measurements, a 3 dB rise or fall represents a doubling or halving, and the appropriate formula is
![]() .
.
Sound intensity measures the sound power flow per square metre. It has been suggested that a 10 dB change of intensity is the equivalent of one step up or down musical dynamic levels. Thus if 60 dB was the equivalent of mp, 70 dB would relate to mf, 80 dB f, and so on. Unfortunately, this is rather too crude a comparison to be of much use, for the intensity level which might be regarded as a musical forte in, say, a string quartet piece written in the late eighteenth century, and performed in a small room, might be heard as mezzo piano or even piano when played by a large orchestra in a concert hall.
The ear does not respond equally to sounds of all frequencies. As we noted earlier, its very construction means that certain frequencies, especially those around 3500 Hz, will be boosted. In fact, particularly at lower levels, high- and low-frequency sounds must be amplified considerably to seem as loud as these mid-frequency sounds. Thus, for example, the sound pressure level of a 20 Hz pure tone (sine wave) needs on average to be around 80 dB to sound as loud as a 3500 Hz tone whose pressure level is 20 dB. Acousticians and psychologists of perception tend to use equal-loudness or Fletcher-Munson curves (or contours) to demonstrate the ear's differing sensitivities to audio frequencies.
Once sound waves have been converted to electrical impulses, they pass via the 'older' regions of the brain inherited from our primitive ancestors further down the evolutionary tree, to 'newer' cortical regions near the surface of the brain. The main areas for auditory information are in the left temporal lobe which mainly deals with speech and language, and possibly the right temporal lobe for musical information, though both areas share processing, and people who have suffered strokes in one of these areas have in many cases been able to compensate by using the other side. It is in the cortex that the processing takes place, which at the highest level, allows us to integrate all the frequency and intensity information, and almost magically interpret it as 'music'.
Comparing musical and scientific terminology
If the scientific and musical terms are compared it can be seen that while they have common ground, a number of distinctions can be made between them. Four basic musical 'dimensions' are pitch, loudness, tone colour, and articulation, which relate to frequency, amplitude or intensity, spectrum and envelope. While the first three of the latter terms have already been mentioned, it is worth considering in a little detail the concept of an amplitude envelope, for it is a term which is widely applied in synthesis.
An envelope is a description or a graph of a sound's dynamic evolution over time, and may have a number of stages. For example, a piano key when struck loudly has a rapid attack, the first part of an envelope. This is usually the most complex and quickly changing stage, in which the different frequencies from the harmonic series which make up the sound enter and evolve gradually. The relation between this part of the sound, which can appear to have a substantial noise component, and the rest of it, can be compared to that between a consonant at the start of a word and vowels which follow. The attack assists the localization of a sound, making it is easier for the listener to deduce the direction from which it is coming, and to discriminate the start points of individual notes. The sound will then decay fairly rapidly to a relatively steady-state sustain segment while the finger is held over the note (though there will be a gradual decrease in intensity over time). Finally, when the finger is lifted off the key, comes the release stage, as the volume falls to silence, which may be more or less instantaneous depending upon the acoustic of the performing space, and the amount of damping in the instrument.
This description, whilst conforming to the terminology used by many synthesizer manufacturers, gives a much cruder impression of how sound changes in many acoustic instruments than is really the case. Figure 10 illustrates just such a basic envelope associated with an idealized piano sound.
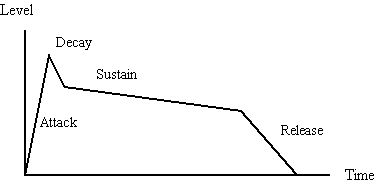
Figure 10. An idealized amplitude envelope for a piano tone.
Musical pitch is obviously related to frequency, but the two terms are by no means synonymous. When low- or high-frequency notes are played at different dynamic levels, their apparent pitch can appear to change, at least to some individuals. In the region of 1000 Hz to 2000 Hz loudness differences seem to have little effect on pitch, while at lower frequencies pitch can seem to fall, and higher frequencies appear to rise, in both cases by up to 5%. Interestingly, it has been discovered that many people prefer octaves to be tuned slightly larger the 2:1 frequency ratio of the harmonic series. Roederer observes the tendency of string players and singers to slightly sharpen the upper notes of the intervals of a major third and major sixth relative to those of 'modern' equal-tempered tuning.
This latter point about the nature of equal-tempered tuning merits further discussion. It is possible to tune the notes of, say, a C major scale by using the intervals derived from the harmonic series. The ratios between the intervals found in the harmonic series are multiplied by the frequency of the starting note, to build up the scale step by step. As can be seen in Figure 11, the first two notes of the harmonic series on C2 lie an octave apart, and their numbers in the series are one and two, thus the ratio of the higher note to the lower is 2:1. A perfect fifth is found between harmonics two and three, yielding the ratio 3:2, and a perfect fourth between harmonics four and three (4:3). Using this method it is possible to derive a complete diatonic scale which is consonant with the harmonic series. Unfortunately this tuning system (which is called Just intonation) has the unfortunate properties of having two different sizes of major second, and several other intervals between its members which are out of tune with the harmonic series.
C2 C3 G3 C4 E4 G4 Bb4 C5 D5 E5 F#5 G5 A5 Bb5 B5
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Figure 11. The first fifteen harmonics of a harmonic series on C2.
A partial solution to this problem was provided by so-called Pythagorean tuning which uses the perfect intervals of the fourth, fifth and octave to form a scale (the sequence of tuning for C major is C - G - [C - F] - D - A - E - B). This scale has just one form of each of the major and minor seconds, and as a diatonic mode is rather 'sweet' and effective, but when extended to a chromatic form introduces a number of problems which make modulation awkward.
The modern system of equal temperament is a compromise in which only the octave is in tune with the harmonic series. The tuning method, which is not quite the same as the one described by Bach as 'well tempered', makes all intervals of a semitone equal in size, slightly flatter than that found in just intonation and slightly sharper than that of Pythagorean tuning. This has a major implication: on grounds of convenience, a tuning system has been adopted which is in conflict with 'nature'. We have thus become accustomed to regard as natural a system in which the intervals used to form chords are out of tune with the harmonics found in the component notes, which are thus inherently dissonant. This is a further example of the balance between order and disorder, nature and artifice, which animates music.
The notation of pitch is generally somewhat inexact - few composers have attempted to create scores which accurately map the microtonal deviations which are such an essential part of a performance. Staff notation is quickly and easily readable, and offers the performer considerable freedom of interpretation, but does not precisely indicate actual frequency changes. There are examples of notations which attempt to accurately describe performances, such as Bartók's transcriptions of Yugoslavian folk songs. These are so detailed, however, that it is hard to imagine that they could be accurately reproduced by any normal performer.
Pitch is not permanently locked to any fixed frequency standard. For long periods of musical history there existed for pitch the equivalent of local time, where musical establishments such as orchestras and churches would decide on their own standard, for example, the tuning of A4 on the organ could vary by more than a minor third each way. Works such as Beethoven's Missa Solemnis, would have been originally sung at a pitch which is around one semitone lower than that used today, which accounts to some extent for the difficulties that choruses and soloists encounter in it. The modern system, agreed at an International Conference held in London in 1939, sets A4 to 440 Hz, and this has universally been adopted. Some institutions, and in particular some European opera houses, have embraced higher tuning standards in order in order to achieve a greater brilliance.
It has already been indicated that the term loudness and its scientific analogues are not identical in meaning. Depending upon its frequency, the same intensity or sound pressure level may result in a sound which is either quite loud or inaudible. Whereas loudness, like pitch, is largely a subjective response in the performer or listener which is contingent upon many musical and extra-musical factors, intensity and sound pressure are objectively measurable phenomena. Terms like piano and forte, as mentioned before, are not absolute measurements, but gain their meaning according to their context. A notation which accurately set out the rise and fall of the dynamic levels in music would probably be unreadable, and would be resisted by performers as an attempt to emasculate them.
The perceived loudness of a musical sound is also dependent upon the relative level of noise which may be masking or covering it, and the dynamic range of the music. Television advertisements often appear to be much louder than the programs surrounding them, but generally they are not broadcast at a higher level, but with a very small dynamic range: to use the technical term, they are heavily compressed, with little difference between louds and softs. This is also a feature of much broadcast popular music (and increasingly, classical music) especially when the intended audience is listening in a noisy environment like a car.
Articulation signs such as accents, stresses, staccato marks and hairpins are aides memoire used to indicate the alteration in the dynamic contour of a note to the musician. Their meaning is connected both to the historic location of the score (for example, a staccato dot may mean something rather different to a keyboard player performing a Haydn sonata than to a violinist playing a work by Stravinsky), and the instrument on which they are performed (the stress sign has a different implication to for a clarinetist than a pianist). In contrast, the amplitude envelope of a note is a measurement of the effects both of the articulation applied by the performer, and the normal characteristics of the instrument. It is not a symbol to be realised, but a description of the realisation of the symbol. Indeed the use of regular envelopes in electronic synthesis can be irritating because of the uniformity of the sound which results; the perpetually changing envelopes of natural instruments is a source of their fascination, an example of the randomness and chaos which is a fundamental ingredient in the microstructure of music.
Musicians tend to mean two slightly different things when they use the terms timbre or tone colour. In one sense the term refers to the totality of the sound - those characteristics which makes us describe it as horn, flute, or violin like. In another sense it refers to the quality of the sound: its closeness to an elusive and ill-defined 'good tone'. Musical notation provides almost no means of marking changes of timbral quality - it is assumed that, by reference to common practice and convention, performers will be able to deduce the most suitable tone colour for a particular part of a composition. The terminology which is available, such as cantabile ('with a singing tone') is often less than specific about how the instrumentalist is intended to produce the effect.
By investigating the spectra of sounds, we may be able to deduce common factors between instruments which are regarded as particularly fine, but in themselves the spectra are not of much value in determining aesthetic quality. The analysis of the components of a sound will never explain the effect of the sound, which is as much to do with the psychological and experiential make up of the listener as inherent properties. They do show, however, that instrumental timbres are not static, but are continually changing, and contain essential noise elements - a constant tone colour, like an invariant envelope, would probably be felt to be uninteresting and dull by the critical listener.
It is probably best to regard the two sets of terminology, musical and scientific, the one subjective and imprecise, the other objective and exact, as complementary. To the musician, the language of acoustics may seem clinical and remote, detached from emotion which many feel to be central to performance activities. Such suspicions are unwarranted, for it provides a context in which the microstructure of music can be explored in parallel with the appreciative, music-analytic, and critical approaches, and in which the skills of music technology can be developed with sympathetic understanding of the relation between nature, art and science.
Reference
Moore, An Introduction to the Psychology of Hearing